Fibonacci and other number sequences
Consider this set of numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,..... how would you define this series?
If you observe carefully you can find that every number is the sum of its previous two numbers
0 + 1 = 1
1 + 1 = 2
2 + 1 =3
3 + 2 = 5 and so on. These are known as Fibonacci Numbers or the Fibonacci Sequence. This sequence is surprisingly found every where in nature like the spiral arrangement of pineapples, the seeds of a sunflower or the arrangement in a pine cone.
Who was this Fibonacci?
He was a 13th century Italian mathematician who wrote a hugely influential book called “Liber Abaci” ("Book of Calculation"), in which he promoted the use of the Hindu-Arabic numeral system, describing its many benefits for merchants and mathematicians alike over the clumsy system of Roman numerals then in use in Europe.
Before Fibonacci wrote his work, the sequence Fn had already been discussed by Indian scholars, who had long been interested in rhythmic patterns that are formed from one-beat and two-beat notes. The number of such rhythms having n beats altogether is Fn+1; therefore both Gospala (before 1135) and Hemachandra (c. 1150) mentioned the numbers 1, 2, 3, 5, 8, 13, 21, … explicitly.
the Fibonacci or the Hemachandra numbers, there are other interesting patterns formed with numbers.
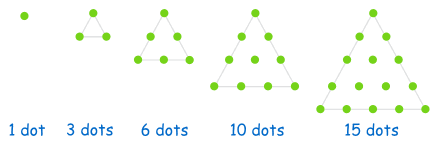
Triangular Numbers
Pattern - Add the next integer to the bottom and count the dots.
Squares
Pattern - add increasing odd numbers to get the next number or product of a number multiplied by itself.
Cubes
Pattern - product of a number multiplied by itself 3 times.
No comments:
Post a Comment