Algebra - INTRO STORY (1) - Bijaganitha

The seed counting - by Bhaskara The Teacher

Bhaskaracharya was a 12th century Mathematician, born in modern day Karnataka. He was one of the original thinkers who wrote on mathematics. A medieval inscription in an Indian temple reads:-

Triumphant is the illustrious Bhaskaracharya whose feats are revered by both the wise and the learned. A poet endowed with fame and religious merit, he is like the crest on a peacock.

Bhaskaracharya wrote the Siddhānta Śiromani (1150 AD), a treatise on mathematics when he was 36 years old. It is divided into 4 parts and can be considered as separate works. 

Imagine math written in a poetic language and named as "The Beautiful". Well, its the Lilavati. The name of the book comes from his daughter, Lilāvati. The book contains thirteen chapters, 278 verses, mainly arithmetic and measurement.
Bijaganita It is divided into six parts, contains 213 verses and is devoted to algebra. It was the first text to recognize that a positive number has two square roots (a positive and negative square root).
Ganitadhyaya and Goladhyaya are devoted to astronomy. All put together there are about 900 verses.(Ganitadhyaya has 451 and Goladhyaya has 501 verses).

Note: 12th century was a important period in the history of mathematics. It is the time when trade was flourishing with the East, and Eastern knowledge gradually began to spread to the West. Indian numerals were modified by Arab mathematicians to form the modern Hindu-Arabic numeral system (used universally in the modern world).

Introduction to Algebra

Algebra is the Language of Mathematics

Algebra is one of the most important and interesting topics in middle school mathematics. Here children understand the use of unknowns, with practical application in their daily lives. Experience of understanding algebra at school goes a long way in the kind of liking/hatred one will develop as an adult towards mathematics. So it is very important for the teacher to first understand the concept and help students interpret the same.

There are 3 important things I should understand as a teacher when preparing to introduce algebra
1. Algebra is the generalization or abstraction of arithmetic.
2. It is clearly the pure language of mathematics, which requires knowledge of  the mathematical vocabulary (symbols and variables) and grammar (algebraic rules)
3. Algebra is a tool for mathematical modeling (solving real world problems)

The effective way to introduce algebra at middle school is by recollecting something students already know (interlinking subjects) or using an activity.

Algebra has been an inevitable part, in the growth of different civilizations. Following is a mind map of the respective contributions.

(The teacher might or might not elaborate on the different contributions. But can give it as group assignments to initiate research/ exploratory learning among the students)

(Click on the image to enlarge.)

Suares, Cubes and their Roots - INTRO STORY (1)

Fibonacci and other number sequences

Consider this set of numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,..... how would you define this series?

If you observe carefully you can find that every number is the sum of its previous two numbers

0 + 1 = 1

1 + 1 = 2

2 + 1 =3

3 + 2 = 5 and so on. These are known as Fibonacci Numbers or the Fibonacci Sequence. This sequence is surprisingly found every where in nature like the spiral arrangement of pineapples, the seeds of a sunflower or the arrangement in a pine cone.

Who was this Fibonacci?

He was a 13th century Italian mathematician who wrote a hugely influential book called “Liber Abaci” ("Book of Calculation"), in which he promoted the use of the Hindu-Arabic numeral system, describing its many benefits for merchants and mathematicians alike over the clumsy system of Roman numerals then in use in Europe.

Before Fibonacci wrote his work, the sequence Fn had already been discussed by Indian   scholars, who had long been interested in rhythmic patterns that are formed from one-beat and two-beat notes. The number of such rhythms having n beats altogether is Fn+1; therefore both Gospala (before 1135) and Hemachandra (c. 1150) mentioned the numbers 1, 2, 3, 5, 8, 13, 21, … explicitly.

the Fibonacci or the Hemachandra numbers, there are other interesting patterns formed with numbers.

Triangular Numbers

Pattern - Add the next integer to the bottom and count the dots.

Squares 

Pattern - add increasing odd numbers to get the next number or product of a number multiplied by itself.

Cubes 

Pattern - product of a number multiplied by itself 3 times.

EXPONENTS AND POWERS - INTRO STORY (2)

The Story of Googol and Googolplex

A googol is a large number equal to  (i.e., a 1 with 100 zeros following it). 

Written out explicitly,
10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Edward Kasner (April 2, 1878 – January 7, 1955) was a prominent American mathematician who was appointed Tutor on Mathematics in the Columbia University Mathematics Department.
In 1940, with James R. Newman, Kasner co-wrote a non-technical book surveying the field of mathematics, called Mathematics and the Imagination. It was in this book that the term "googol" was first introduced:

 If you start reading the book at the beginning, you'll come to the first chapter, titled "New Names For Old." Here is the relevant passage about the invention of the words "googol" and "googolplex":

"Words of wisdom are spoken by children at least as often as by scientists. The name 'googol' was invented by a child (Dr. Kasner's nine-year-old nephew) who was asked to think up a name for a very big number, namely, 1 with a hundred zeros after it. He was very certain this number was not infinite, and therefore equal certain that it had to have a name. At the same time he that he suggested 'googol' he gave a name for a still larger number: 'Googolplex.' A googolplex is much larger than a googol, but is still finite, as the inventor of the name was quick to point out. It was first suggested that a googolplex should be 1, followed by writing zeros until you got tired. This is a description of what would happen if one actually tried to write a googolplex, but different people get tired at different times and it would never do to have Carnera a better mathematician than Dr. Einstein, simply because he had more endurance. The googolplex then, is a specific finite number, with so many zeros after the 1 that the number of zeros is a googol. A googolplex is much bigger than a googol, much bigger even than a googol times a googol. A googol times a googol would be 1 with 200 zeros, whereas a googolplex is 1 with a googol of zeros. You will got some idea of the size of this very large but finite number from the fact that there would not be enough room to write it, if you went to the farthest star, touring all the nebulae and putting down more zeros every inch of the way."

--MATHEMATICS AND THE IMAGINATION, Kasner and Newman, page 23.

Lets us explore the concept of exponents...

EXPONENTS AND POWERS - INTRO STORY (1)

Exponential Growth and the Legend of Paal Paysam

Exponential Growth is an immensely powerful concept. To help us grasp it better let us use an ancient Indian chess legend as an example.

The legend goes that the tradition of serving Paal Paysam to visiting pilgrims started after a game of chess between the local king and the lord Krishna himself.

The king was a big chess enthusiast and had the habit of challenging wise visitors to a game of chess. One day a traveling sage was challenged by the king. To motivate his opponent the king offered any reward that the sage could name. The sage modestly asked just for a few grains of rice in the following manner: the king was to put a single grain of rice on the first chess square and double it on every consequent one.
Having lost the game and being a man of his word the king ordered a bag of rice to be brought to the chess board. Then he started placing rice grains according to the arrangement: 1 grain on the first square, 2 on the second, 4 on the third, 8 on the fourth and so on:

Following the exponential growth of the rice payment the king quickly realized that he was unable to fulfill his promise because on the twentieth square the king would have had to put 1,000,000 grains of rice. On the fortieth square the king would have had to put 1,000,000,000 grains of rice. And, finally on the sixty fourth square the king would have had to put more than 18,000,000,000,000,000,000 grains of rice which is equal to about 210 billion tons and is allegedly sufficient to cover the whole territory of India with a meter thick layer of rice. At ten grains of rice per square inch, the above amount requires rice fields covering twice the surface area of the Earth, oceans included.
It was at that point that the lord Krishna revealed his true identity to the king and told him that he doesn't have to pay the debt immediately but can do so over time. That is why to this day visiting pilgrims are still feasting on Paal Paysam and the king's debt to lord Krishna is still being repaid.

Source
http://www.singularitysymposium.com/exponential-growth.html

The simple, brute-force solution is to just manually double and add each step of the series:

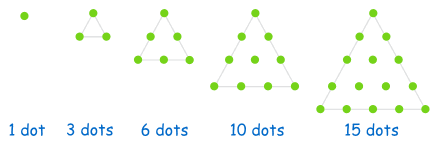
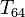where  is the total number of grains.

The series may be expressed using exponents:

So lets explore the concept of exponents and powers

There is another version of this story in Islamic Literature  http://quatr.us/islam/literature/chesswheat.htm

RATIONAL NUMBERS - INTRO STORY (2)

What does the word "Rational" mean?

Well the dictionary says:
 /'in accordance with the principles of logic or reason; reasonable; of sound mind/'
and the translations are as follows Hindi  विवेकपूर्ण , Tamil பகுத்தறிவு.

Whenever I think of Rationality, this story of Birbal comes to my mind.

One day Akbar asked his courtiers if they could tell him the difference between truth and falsehood in three words or less.
The courtiers looked at one another in bewilderment. "What about you, Birbal?" asked the emperor. "I'm surprised that you too are silent." "I'm silent because I want to give others a chance to speak," said Birbal.

"Nobody else has the answer," said the emperor. "So go ahead and tell me what the difference between truth and falsehood is — in three words or less."

"Four fingers" said Birbal. "Four fingers?" asked the emperor, perplexed. 

"That's the difference between truth and falsehood, your Majesty," said Birbal. "That which you see with your own eyes is the truth. That which you have only heard about might not be true. More often than not, it's likely to be false."

"That is right," said Akbar. "But what did you mean by saying the difference is four fingers?'. "The distance between one's eyes and one's ears is the width of four fingers, Your Majesty," said Birbal, grinning.




A rational number is a number that can be expressed as a fraction or ratio.  
The numerator and the denominator of the fraction are both integers.

An irrational number cannot be expressed as a fraction.

RATIONAL NUMBERS - INTRO STORY (1)

Carl Friedrich Gauss was the famous 17th century German Mathematician. 
His mathematical skills were clearly visible from a very young age. His elementary teacher Büttner, one day asked all his students to add numbers from one to hundred. this was to keep them engaged for some time. So the students started summing up the numbers,
 1 + 2 + 3 + 4 + ............... + 100
Within minutes Gauss was sitting idle. The teacher asked why he was not doing the sum, for which he replied he's already finished it! and the answer is 5050.
Wonder how he did that? Gauss observed that there is a pattern in these numbers, 
1 + 100 = 101
2 + 99   = 101
3 + 98   = 101
.
.
.
.
50 + 51   = 101
so there are 50 pairs of 101. i.e 50 x 101 = 5050. interesting isn't it? 

Now try this, 

Find the sum of integers from -10 to 10. what will be your approach?
Can you apply the same for adding consecutive fractions? what do you observe?

We are going to study more operations on fractions and integers combined together, called Rational Numbers (Q). Hope you remember the Number System and where Rational numbers fall!.

 A rational number is a number that can be expressed as a fraction  where  and  are integers and . A rational number  is said to have numerator  and denominator . Here, the symbol  derives from the German word Quotient, which can be translated as "ratio,"

A Story For a Topic in Math

It is wonderful to open your math class with a story. My children always appreciated the little tit bits of information along with the regular class. It helps even more when you have a math class just after the PT or lunch time. Am going to record here relevant stories and mind maps for every chapter for classes 8, 7 and 6 in that particular order.
Its also my firm belief that every math teacher and student should know about who discovered a concept or how it evolved - to - what you are learning about it - how it is applied today.
not very difficult for the middle school curriculum.